One of the most commonly used techniques of unsupervised learning is clustering. As the name suggests, clustering is the act of grouping data that shares similar characteristics. In machine learning, clustering is used when there are no pre-specified labels of data available, i.e. we don’t know what kind of groupings to create.
The goal is to group together data into similar classes such that:
Intra-class similarity is high
Inter-class similarity is low
There are two main types of clustering — K-means Clustering and Hierarchical Agglomerative Clustering. In case of K-means Clustering, we are trying to find k cluster centres as the mean of the data points that belong to these clusters. Here, the number of clusters is specified beforehand, and the model aims to find the most optimum number of clusters for any given clusters, k. For this post, we will only focus on K-means.
We are using the minute weather dataset from Kaggle which contains weather-related measurements like air pressure, maximum wind speed, relative humidity etc. The data was captured in San Diego, over a three-year period from Sept 2011 to Sept 2014 and contains raw sensor measurements captured at one-minute intervals.
The first step is to import necessary libraries…
import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns import sklearn from sklearn.preprocessing import StandardScaler from sklearn.cluster import KMeans from sklearn import metrics from sklearn.cluster import AgglomerativeClustering
…and the dataset
df = pd.read_csv('minute_weather.csv')
df.head()
Exploring our data, we find there are 1,587,257 rows and 13 columns! Since this dataset is quite large, we need to take random samples. Additionally, for the K-means method it is essential to find the positioning of the initial centroids first so that the algorithm can find convergence. To do this, instead of working with the entire dataset, we draw up a sample and run short runs of randomly initialised centroids and track improvements in the metric. A very good explanation of this methodology is given here.
Taking a sample from every 10th row, we create a new sample dataframe
sample_df = df[(df['rowID'] % 10) == 0] sample_df.shape
which yields 158726 rows and 13 columns (much better!)
Checking for null values, we find rain_accumulation and rain_duration can be dropped
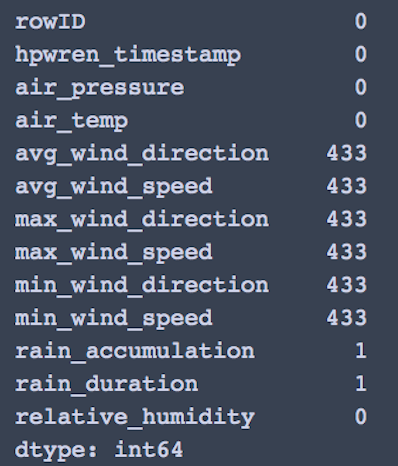
df1 = sample_df.drop(columns =['rain_accumulation','rain_duration']) print(df1.columns)

Between the two values — max wind speed / direction and min wind speed / direction, I have chosen only max for the purposes of clustering as we already have the average values for both. The min values can also be included in the analysis if one chooses to. Finally, the columns we are interested in clustering can be sorted into a new dataframe like this -
cols_of_interest = ['air_pressure', 'air_temp', 'avg_wind_direction', 'avg_wind_speed','max_wind_direction',
'max_wind_speed', 'relative_humidity']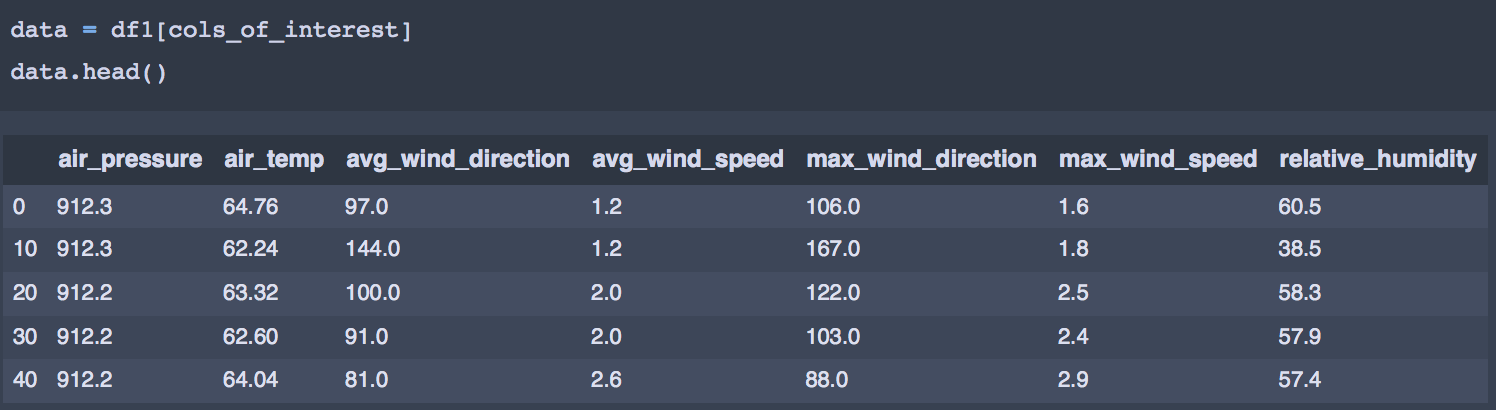
The next step is to scale our values to give them all equal importance. Scaling is also important from a clustering perspective as the distance between points affects the way clusters are formed.
Using the StandardScaler, we transform our dataframe into the following numpy arrays
X = StandardScaler().fit_transform(data) X
K-means clustering
As mentioned before, in case of K-means the number of clusters is already specified prior to running the model. We can choose a base level number for K and iterate to find the most optimum value. To evaluate which number of clusters is more optimum for our dataset, or find cluster fitness we use two scoring methods — Silhouette Coefficient and Calinski Harabasz Score. In reality, there are many different scoring methods depending on what metrics matter most in a model. Usually one method is chosen as the standard but for the purpose of this analysis I have used two.
The Silhouette Coefficient is calculated using the mean intra-cluster distance (a) and the mean nearest-cluster distance (b) for each sample. The Silhouette Coefficient for a sample is (b-a) / max(b-a)
The Calinski Harabasz Score or Variance Ratio is the ratio between within-cluster dispersion and between-cluster dispersion
Let us implement the K-means algorithm using sci-kit learn.
n_clusters= 12
#Set number of clusters at initialisation time k_means = KMeans(n_clusters=12) #Run the clustering algorithm model = k_means.fit(X) model #Generate cluster predictions and store in y_hat y_hat = k_means.predict(X)
Calculating the silhouette coefficient…
from sklearn import metrics labels = k_means.labels_ metrics.silhouette_score(X, labels, metric = 'euclidean')
0.2405
…and the CH score
metrics.calinski_harabasz_score(X, labels)
39078.93
Let us try this for another randomly chosen value i.e. n_clusters = 8
k_means_8 = KMeans(n_clusters=8) model = k_means_8.fit(X) y_hat_8 = k_means_8.predict(X)
Once again, calculating the silhouette coefficient and CV scores
labels_8 = k_means_8.labels_ metrics.silhouette_score(X, labels_8, metric = 'euclidean')
Silhouette coefficient = 0.244
metrics.calinski_harabasz_score(X, labels_8)
CV score = 41105.01
We can see that for both types of scores, 8 clusters gives a better value. However we will have to do several iterations with different number of clusters to find the optimal one. Instead, we can use something called an elbow plot to find this optimal value.
An elbow plot shows at what value of k, the distance between the mean of a cluster and the other data points in the cluster is at its lowest.
Two values are of importance here — distortion and inertia. Distortion is the average of the euclidean squared distance from the centroid of the respective clusters. Inertia is the sum of squared distances of samples to their closest cluster centre.
#for each value of k, we can initialise k_means and use inertia to identify the sum of squared distances of samples to the nearest cluster centre
sum_of_squared_distances = []
K = range(1,15)
for k in K:
k_means = KMeans(n_clusters=k)
model = k_means.fit(X)
sum_of_squared_distances.append(k_means.inertia_)Remember we care about intra-cluster similarity in K-means and this is what an elbow plot helps to capture.
plt.plot(K, sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('sum_of_squared_distances')
plt.title('elbow method for optimal k')
plt.show()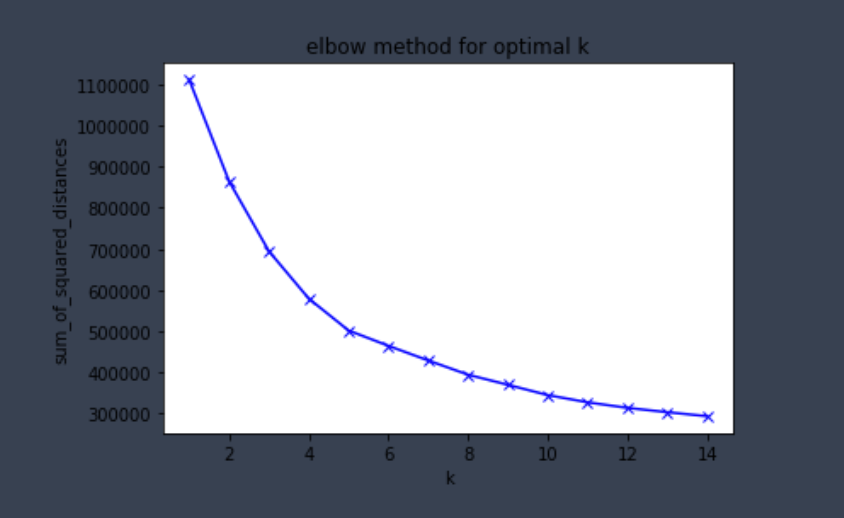
Here we can see the drop in the sum of squared distance starts to slow down after k=5. Hence 5 is the optimal number of clusters for our analysis.
We can verify this by calculating the silhouette coefficient and CH score for k=5.
k_means_5 = KMeans(n_clusters=5) model = k_means_5.fit(X) y_hat_5 = k_means_5.predict(X) labels_5 = k_means_5.labels_ metrics.silhouette_score(X, labels_5, metric = 'euclidean') metrics.calinski_harabasz_score(X, labels_5)
Silhouette coefficient = 0.261
CV score = 48068.32
Both the values are higher than they were for our earlier clusters 12 and 8. We can conclude that k=5 is our optimal number of clusters.
Lastly, we can see the values that are contained in each of our clusters. Using this function, I have created a utility plot.
#function that creates a dataframe with a column for cluster number
def pd_centers(cols_of_interest, centers):
colNames = list(cols_of_interest)
colNames.append('prediction')
# Zip with a column called 'prediction' (index)
Z = [np.append(A, index) for index, A in enumerate(centers)]
# Convert to pandas data frame for plotting
P = pd.DataFrame(Z, columns=colNames)
P['prediction'] = P['prediction'].astype(int)
return P
P = pd_centers(cols_of_interest, centers)
PFor further reading :
- https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
- https://www.kaggle.com/prakharrathi25/weather-data-clustering-using-k-means/notebook
- https://www.datasciencecentral.com/profiles/blogs/python-implementing-a-k-means-algorithm-with-sklearn
- https://blog.cambridgespark.com/how-to-determine-the-optimal-number-of-clusters-for-k-means-clustering-14f27070048f
WRITTEN BY
Data Scientist passionate about finding the narrative within numbers. Curious about brands and human behaviour.
